Работа асинхронного двигателя под нагрузкой.

В рабочем режиме ротор двигателя вращается с частотой n2, меньшей частоты n1 магнитного поля статора, вращающегося в том же направлении, что и ротор.
Поэтому магнитное поле, имеющее большую частоту, скользит относительно ротора с частотой (об/мин), равной разности частот поля и ротора, т. е. ns = n1 - n2.

Относительное отставание ротора от вращающегося магнитного поля статора характеризуется скольжением S.
Скольжение представляет собой отношение разности частот вращения магнитного поля статора и вращающегося ротора к частоте поля статора
S = ns/n1 = (n1 - n2)/n1.
Эта формула определяет скольжение в относительных единицах.Скольжение может быть также выражено в процентах:
S = ((n1 - n2)/n1) x 100%.
Если ротор неподвижен (n2 = 0), то скольжение равно единице или 100%.

Если ротор вращается синхронно с магнитным полем, т. е. с одинаковой частотой
(n2 = n1), то скольжение равно нулю.

Таким образом, чем больше частота вращения ротора, тем меньше скольжение.
В рабочем режиме асинхронного двигателя скольжение мало.
У современных асинхронных двигателей скольжение при полной нагрузке составляет 3—5%, т.е. ротор вращается с частотой, незначительно отличающейся от частоты магнитного поля статора.
При холостом ходе, т. е. при отсутствии нагрузки на валу, скольжение ничтожно мало и может быть принято равным нулю.
Частоту вращения ротора можно определить из следующих соотношений:
n2 = n1 - ns = n1(1 - S) = (60f1/p)(1 - S).

Двигатель будет работать устойчиво с постоянной частотой вращения ротора при равновесии моментов, т. е. если вращающий двигателя М будет равен тормозному моменту на валу двигателя Мт, который развивает приемник механической энергии, например резец токарного станка. Следовательно, можно записать: М = Мт.

Любой нагрузке машины соответствует определенная частота вращения ротора n2 и определенное скольжение S.
Магнитное поле статора вращается относительно ротора с частотой ns и индуктирует в его обмотке эдс Е2, под действием которой по замкнутой обмотке ротора проходит ток I2.
Если нагрузка на валу машины увеличилась, т. е. возрос тормозной момент, то равновесие моментов будет нарушено, так как тормозной момент окажется больше вращающего.
Это приведёт к уменьшению частоты вращения ротора, а следовательно, к увеличению скольжения. С увеличением скольжения магнитное поле будет пересекать проводники обмотки ротора чаще, эдс E2, индуктированная в обмотке ротора, возрастет, а в результате как ток в роторе, так и развиваемый двигателем вращающий момент.

Скольжение и ток в роторе будут увеличиваться до значений, при которых вновь наступит равновесие моментов, т. е. вращающий момент станет равным тормозному.

Так же протекает процесс изменения частоты вращения ротора и развиваемого момента при уменьшении нагрузки двигателя. С уменьшением нагрузки на валу двигателя тормозной момент становится меньше вращающего, что приводит к увеличению частоты вращения ротора или к уменьшению скольжения.

В результате уменьшаются эдс и ток в обмотке ротора, а следовательно, и вращающий момент, который вновь становится равным тормозному моменту.

Магнитное поле статора пересекает проводники обмотки статора и индуктирует в ней эдс Е1, которая уравновешивает приложенное напряжение сети U1.

Если пренебречь падением напряжения в сопротивлении обмотки статора, которое мало по сравнению с эдс, то между абсолютными значениями приложенного напряжения и эдс обмотки статора можно допустить приближенное равенство, т. е.
U1 = E1.

Таким образом, при неизменном напряжении сети будет неизменна и эдс обмотки статора. Следовательно, магнитный поток в воздушном зазоре машины, так же как в трансформаторе, при любом изменении нагрузки остается примерно постоянным.

Ток обмотки ротора создает свое магнитное поле, которое направлено противоположно магнитному полю тока обмотки статора. Чтобы результирующий магнитный поток в машине оставался неизменным при любом изменении нагрузки двигателя, размагничивающее магнитное поле обмотки ротора должно быть уравновешено магнитным полем обмотки статора. Поэтому при увеличении тока в обмотке ротора увеличивается и ток в обмотке статора.

Таким образом, асинхронный двигатель подобен трансформатору, у которого при увеличении тока во вторичной обмотке увеличивается ток в первичной обмотке.

Вращающий момент асинхронного двигателя.

Вращающий момент асинхронного двигателя создается при взаимодействии вращающегося магнитного поля статора с токами в проводниках обмотки ротора. Поэтому вращающий момент зависит как от магнитного потока статора Фm, так и от тока в обмотке ротора I2.
Однако в процессе преобразования энергии (создании вращающего момента) участвует только активная мощность, потребляемая машиной из сети. Вследствие этого вращающий момент зависит не от тока в обмотке ротора I2, а только от его активной составляющей, т. е. I2Xcos2, где 2 - фазный угол между эдс и током в обмотке ротора.
Таким образом, вращающий момент асинхронного двигателя определяется следующим выражением:
М = С Фm I2 cos2,
где С - конструктивная постоянная машины, зависящая от числа ее полюсов и фаз, числа витков обмотки статора и конструктивного выполнения обмотки.

При условии постоянства приложенного напряжения магнитный поток остается также почти постоянным при любом изменении нагрузки двигателя.
Таким образом, в выражении вращающего момента величины Фm и С постоянны и вращающий момент пропорционален только активной составляющей тока в обмотке ротора, т. е. M ~ I2cos2.
Изменение нагрузки или тормозного момента на валу двигателя изменяет частоту вращения ротора и скольжение, что вызовет изменение как тока в роторе I2, так и его активной составляющей I2 cos2.
Можно ток в роторе определить отношением эдс к полному сопротивлению, т. е.
I2 = E2/Z2 = E2/(R + X) и cos2 = R2/(R + X),
где Z2, R2 и X2 — полное, активное и реактивное сопротивления фазы обмотки ротора.

Вместе со скольжением изменяется частота тока ротора.
При неподвижном роторе (n2 = 0 и S = 1) вращающееся поле с одинаковой частотой пересекает проводники обмотки статора и ротора и частота тока в роторе равна частоте тока в сети (f2 = f1).
При уменьшении скольжения обмотка ротора пересекается магнитным полем с меньшей частотой, так что частота тока в роторе уменьшается. Когда ротор вращается синхронно с полем (n2 = n1 и S = 0), проводники обмотки ротора не пересекаются магнитным полем, так что частота тока в роторе равна нулю f2 = 0. Таким образом, частота тока в роторе пропорциональна скольжению, т. е. f2 =Sf1.
Активное сопротивление обмотки ротора почти не зависит от частоты, тогда как эдс и реактивное сопротивление пропорциональны частоте, т. е. изменяются с изменением скольжения, и могут быть определены следующими выражениями:
E2 = SE и X2 = SX,
где Е и X — соответственно эдс и индуктивное conpoтивление фазы обмотки неподвижного ротора. Таким образом, имеем:
I2 = SE/(R + (SX)) и cos2 = R2/(R + (SX))
и вращающий момент
M I2cos2 = SER2/(R + (SX))

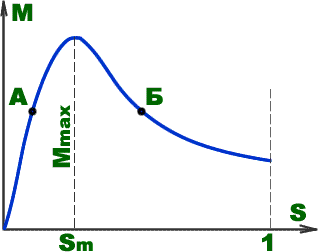
Зависимость вращающего момента
асинхронного двигателя от скольжения

Следовательно, при небольших скольжениях (примерно до 20%), когда SX мало по сравнению с R2, увеличение скольжения вызывает повышение вращающего момента, так как при этом возрастает активная составляющая тока в роторе (I2cos2).
При больших скольжениях (SX>R2) увеличение скольжения будет вызывать уменьшение вращающего момента.
Таким образом, хотя и возрастает ток в роторе I2, но его активная составляющая I2cos2 и, следовательно, вращающий момент уменьшатся вследствие значительного повышения реактивного сопротивления обмотки ротора.
На изо показана зависимость вращающего момента от скольжения.

При некотором скольжении Sm (примерно 20%) двигатель развивает максимальный момент, который определяет перегрузочную способность двигателя и обычно в 2 - 3 раза превышает номинальный момент.
Устойчивая работа двигателя возможна только на восходящей ветви кривой зависимости момента от скольжения, т. е при изменении скольжения в пределах от 0 до Sm. Работа двигателя на нисходящей ветви указанной зависимости, т. е. при скольжении S > Sm невозможна, так как не обеспечивается устойчивое равновесие моментов.
Если предположить, что вращающий момент был равен тормозному (M = МТ) в точках А и Б, то при случайном нарушении равновесия моментов в одном случае оно восстанавливается, а в другом не восстанавливается.

Допустим, что вращающий момент двигателя почему-либо уменьшился (например, при понижении напряжения сети), тогда скольжение начнет увеличиваться.

Если равновесие моментов было в точке A, то увеличение скольжения вызовет увеличение вращающего момента двигателя и он станет вновь равным тормозному моменту, т. е. равновесие моментов восстановится.

Если же равновесие моментов было в точке Б, то увеличение скольжения вызовет уменьшение вращающего момента, который будет оставаться всегда меньше тормозного, т. е. равновесие моментов не восстановится и частота вращения ротора будет непрерывно уменьшаться до полной остановки двигателя.

Если приложить к валу двигателя тормозной момент, больший максимального момента, то равновесие моментов нарушится и ротор двигателя остановится.
Вращающий момент двигателя пропорционален квадрату приложенного напряжения, так как пропорциональны напряжению как магнитный поток, так и ток в роторе. Поэтому изменение напряжения в сети вызывает значительное изменение вращающего момента.

Рабочие характеристики асинхронного двигателя.

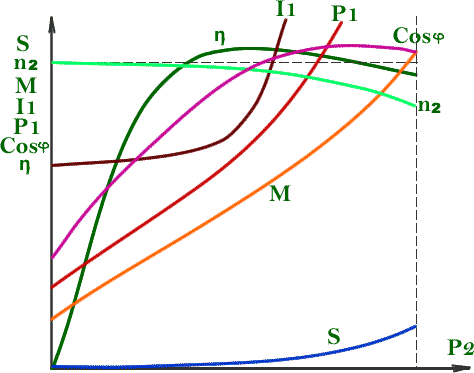
Рабочие характеристики асинхронного двигателя представляют собой зависимости скольжения S, частоты вращения ротора n2, развиваемого момента М, потребляемого тока I1, расходуемой мощности P1, коэффициента мощности cos и кпд от полезной мощности Р2 на валу машины. Эти характеристики (изо) снимаются при естественных условиях работы двигателя, т. е. двигатель нерегулируемый, частота тока f1 и напряжение U1 сети остаются постоянными, а , изменяется только нагрузка на валу двигателя.

При увеличении нагрузки на валу двигателя скольжение возрастает, причем при больших нагрузках скольжение увеличивается несколько быстрее, чем при малых.
При холостом ходе двигателя скольжение очень мало (n2 ~ n1 или S ~ 0).

При номинальной нагрузке скольжение обычно составляет S = 3 - 5% (0,95).

Частота вращения ротора n2 = n1(1—S) = (60f1/p)(1 - S).

При увеличении нагрузки на валу двигателя скольжение возрастает, а частота вращения будет уменьшаться. Однако изменение частоты вращения при увеличении нагрузки от 0 до номинальной очень не значительно и не превышает 5 %. Поэтому скоростная характеристика асинхронного двигателя является жесткой - она имеет очень малый наклон к горизонтальной оси.

Вращающий момент М, развиваемый двигателем, уравновешен тормозным моментом Мт на валу и моментом Мо, идущим на преодоление механических потерь, т. е.
М = Мт + М0 = Р2/2—М0, где Р2 - полезная мощность двигателя, 2 - угловая скорость ротора.

При холостом ходе двигателя М = М0; с увеличением нагрузки на валу вращающий момент также увеличивается, причем за счет некоторого уменьшения частоты вращения ротора увеличение вращающего момента происходит быстрее, чем увеличение полезной мощности на валу.

Рабочие характеристики асинхронного двигателя

Ток I1, потребляемый двигателем из сети, неравномерно изменяется с увеличением нагрузки на валу двигателя.

При холостом ходе cos мал и ток имеет большую реактивную составляющую.

При малых нагрузках на валу двигателя активная составляющая статора меньше реактивной составляющей, поэтому активная составляющая тока незначительно влияет на ток I1, определяющийся в основном реактивной составляющей.

При больших нагрузках активная составляющая тока статора становится больше реактивной и изменение нагрузки вызывает большое изменение тока I1.

Графически зависимость потребляемой двигателем мощности Р1 выражается прямой линией, незначительно отклоняющейся вверх от прямой при больших нагрузках, что объясняется увеличением потерь в обмотках статора и ротора с возрастанием нагрузки.

Коэффициент мощности изменяется в зависимости от нагрузки на валу двигателя следующим образом. При холостом ходе cos мал (порядка 0,2), так как активная составляющая тока статора обусловленная потерями мощности в машине, мала по сравнению с реактивной составляющей этого тока, создающей магнитный поток.

При увеличении нагрузки на валу cos возрастает (достигая наибольшего значения 0,8—0,95) в результате увеличения активной составляющей тока статора.
При очень больших нагрузках происходит некоторое уменьшение cos, так как вследствие значительного увеличения скольжения и частоты тока в роторе возрастает реактивное сопротивление обмотки ротора.

Кривая кпд имеет такой же вид, как в любой машине или трансформаторе. При холостом ходе кпд равен нулю. С увеличением нагрузки на валу двигателя кпд резко увеличивается, а затем уменьшается. Наибольшего значения кпд достигает при такой нагрузке, когда потери мощности в стали и механические потери, не зависящие от нагрузки, равны потерям мощности в обмотках статора и ротора, зависящим от нагрузки.